Разработка методологии проектирования насосно-эжекторных установок с расширенным использованием численных экспериментов
Ю.А. Сазонов, к.т.н. РГУ нефти и газа им. И.М. Губкина
К числу актуальных вопросов относится разработка энергосберегающих технологий. В затратах энергии на добычу, сбор и подготовку нефти и газа значительная доля энергии приходится на насосное оборудование. Для добычи и перекачки газожидкостных смесей и для утилизации газа, помимо объемных и динамических машин, используют насосно-эжекторные установки различных исполнений. Современные компьютерные технологии способствуют экономии финансовых и материальных ресурсов, так как позволяют повысить эффективность работ, связанных с проектированием насосных установок и с подбором оборудования для конкретных условий эксплуатации. В этой связи разработка методологии проектирования и совершенствование математических моделей насосно-эжекторных установок является актуальной задачей.
В практическом плане наибольший интерес представляет сочетание эжектора с многоступенчатым лопастным насосом. При моделировании устанавливают взаимосвязь характеристики эжектора с характеристикой силового насоса, подающего рабочую жидкость в сопло эжектора. В рабочей жидкости в ряде случаев может присутствовать газ. В качестве перекачиваемой среды, в общем случае, рассматривают газожидкостную смесь. Параметр входное газосодержание - β определяют делением объемного расхода газа на объемный расход газожидкостной смеси по условиям на входе эжектора. Поскольку газосодержание β может меняться в широком диапазоне, от 0 до 1, математическая модель насосно-эжекторной установки была разбита на несколько взаимосвязанных блоков-моделей: модель-1 жидкостно-жидкостного эжектора (или струйного насоса) [1]; модель-2 жидкостно-газового эжектора [2]; модель-3 газо-газового эжектора; модель-4 лопастного насоса для жидкостей [3]; модель-5 многоступенчатого лопастного насоса для газожидкостных смесей [4]. На основе моделей 1 и 2 для жидкостно-жидкостного эжектора и жидкостно-газового эжектора разработана модель – 6 для условий перекачки газожидкостных смесей при подаче в сопло эжектора рабочей жидкости. Каждая из моделей позволяет решать гидродинамические задачи: прямые и обратные. Таким образом, шесть моделей, с учетом прямой и обратной задачи, позволяют решать 12 типов задач и моделировать различные условия эксплуатации насосно-эжекторной установки, для различных вариантов компоновок эжектора и силового насоса. Модель-3, в данном случае, выполняет преимущественно вспомогательную роль, при расчете параметров газа и при сравнении различных вариантов насосных и компрессорных установок. Каждая из разработанных моделей может быть использована автономно при расчете струйного аппарата или же лопастной машины (насоса или вентилятора). 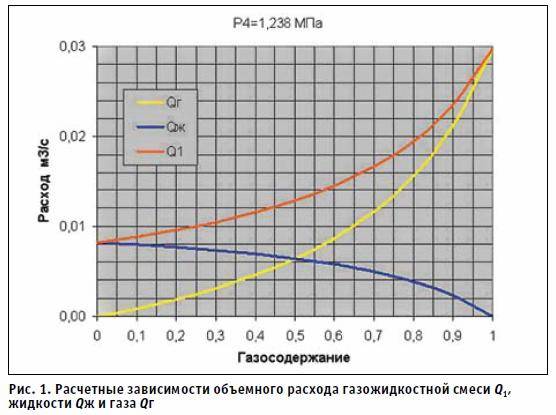
В основу математических моделей заложены известные уравнения гидродинамики и газовой динамики: уравнение неразрывности, уравнение энергии, уравнение количества движения, уравнение моментов количества движения [5].
Основные теоретические разработки и экспериментальные исследования по струйной технике и лопастным насосам выполнены на кафедре «машин и оборудования нефтяной и газовой промышленности» РГУ нефти и газа им. И.М. Губкина.
При использовании модели-6 рассматриваются условия течения газожидкостной смеси, когда скачок давления происходит в пределах цилиндрической камеры смешения. Варианты эжекторов с разрывными гистерезисными характеристиками [6] в данном случае не представлены, как и эжекторы с короткой камерой смешения, поскольку рабочие процессы в этих машинах имеют ряд особенностей, требующих отдельного и более детального рассмотрения. 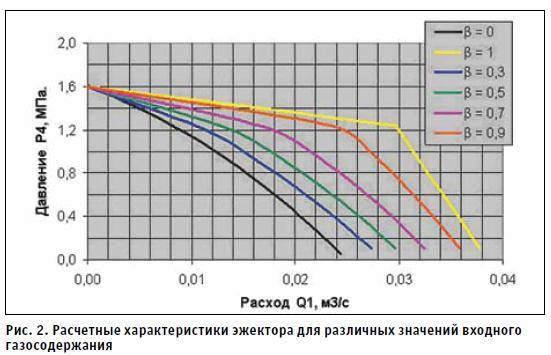
Если газосодержание β на входе эжектора принимает предельное значение 0, то эжектор переходит в режим работы струйного насоса. Если газосодержание β на входе эжектора принимает другое предельное значение 1, то эжектор переходит в режим работы жидкостно-газового эжектора. Для расчета характеристик струйного насоса используют модель-1, а для расчета жидкостно-газового эжектора, соответственно, модель-2. Научный и практический интерес представляет вопрос о возможности применения отмеченных математических моделей 1 и 2 при расчете характеристики эжектора для газожидкостной смеси, с произвольным газосодержанием, от 0 до 1. Если предельные режимы работы эжектора изучены достаточно подробно, то работа эжектора на газожидкостных смесях нуждается в более глубоком изучении. При разработке математической модели для произвольных значений газосодержания, как часто бывает при моделировании, количество неизвестных параметров превышает количество уравнений. В таких случаях разрабатывают гипотезу, чтобы замкнуть систему уравнений. Для данной задачи рассмотрены следующие режимы работы эжектора. Давление газожидкостной смеси на входе эжектора постоянное Р1=idem, давление рабочей жидкости на входе эжектора постоянное Р0=idem, давление газожидкостной смеси на выходе эжектора постоянное Р4=idem. При этом рассматриваем изменение объемного расхода газожидкостной смеси на входе эжектора Q1 в зависимости от значения газосодержания β. Для данных условий модели 1 и 2 позволяют определить два предельных значения: Q1а для β=0 и Q1в для β=1. Соответственно можно рассчитать и два предельных значения КПД: ηа для β=0 и ηв для β=1. Таким образом, при изменении газосодержания β, от 0 до 1, КПД соответственно будет меняться в диапазоне от ηа до ηв. Формулируем новую гипотезу: «при постоянстве давлений Р0 , Р1 , Р4 на координатной плоскости η-Q1 расчетные точки для всех значений газосодержания β ложатся на одну и ту же прямую линию». По мере сбора и обработки экспериментальных данных формулировка гипотезы, естественно, может и будет уточняться. 
Уравнение отмеченной прямой линии составляют по координатам двух характерных точек - (Q1а , ηа) и (Q1в , ηв):
(Q1 - Q1а)/(Q1в - Q1а) = (η – ηа)/(ηв – ηа)
Уравнение (1) позволяет установить зависимость Q1 от газосодержания β и давления Р4:
Q1=C/(A-B)
где:
А=( β* Р1*ln(Р4 /Р1)+(1- β)*( Р4 - Р1))/Q0 /( Р0 – Р4)
B=(ηв – ηа)/ (Q1в - Q1а)
C= ηа - Q1а*B
Для принятых условий постоянства давлений по формулам (2-5) рассчитывают Q1в зависимости от газосодержания β. Пример графического представления результатов расчета показан на рисунке 1.
Рисунок 1 – Расчетные зависимости объемного расхода газожидкостной смеси Q1, жидкости Qж и газа Qг.
Подобные расчеты выполняют для нескольких значений давления Р4 . Для каждого значения Р4 в уравнение (1) вносятся соответствующие изменения, поскольку меняются координаты точек (Q1а , ηа) и (Q1в , ηв). По расчетным данным строят характеристики эжектора для различных значений газосодержания β=idem. На рисунке 2 представлены расчетные характеристики эжектора для нескольких значений газосодержания.
Рисунок 2 – Расчетные характеристики эжектора для различных значений входного газосодержания.
В представленном примере в качестве базовых характеристик были использованы две расчетные характеристики для двух предельных значений газосодержания 0 и 1. Разработанный метод расчета универсален и может применяться также в случаях, когда одна или две характеристики получены экспериментальным путем при перекачке газожидкостных смесей. В общем случае в качестве базовых характеристик используют характеристики «Q1а - Р4» и «Q1в - Р4» (расчетные или экспериментальные) для двух определенных значений газосодержания βа и βв , из диапазона от 0 до 1. Таким образом, при использовании представленной методики объем физических экспериментов может быть уменьшен, а значительную часть информации, о режимах работы эжектора, можно получить при выполнении численных экспериментов.
На основе математической модели-4 разработан высоконапорный насос группы ЭЦН5 с колесом открытого типа. Насос может быть использован автономно или в качестве силового насоса для насосно-эжекторной установки. Одно из исполнений насоса представлено на рисунке 3.
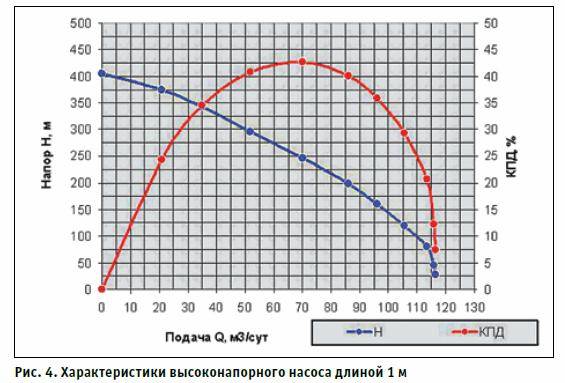
Рисунок 3 – Ступень высоконапорного насоса.
На кафедре «машин и оборудования нефтяной и газовой промышленности» РГУ нефти и газа им. И.М. Губкина выполнены стендовые испытания экспериментальных ступеней различного исполнения. В качестве модельной среды использовали техническую воду. Частота вращения вала насоса 2910 об/мин. На рисунке 4 представлены обработанные результаты испытаний, для насоса длиной 1 м. Учитывая кратное снижение массы рабочего колеса, открывается перспектива дальнейшего повышения напора насоса за счет увеличения частоты вращения вала, при отсутствии серьезных проблем с балансировкой ротора.
Рисунок 4 – Характеристики высоконапорного насоса длиной 1 м.
По результатам выполненных работ можно сделать следующие основные выводы. Учитывая большое разнообразие условий эксплуатации эжекторов и лопастных насосов, работающих раздельно или в общей системе, оказалось оправданным разделение комплексной методики расчета на блоки. В этом случае каждый блок может быть использован также автономно, при выполнении разнообразных проектных работ или же при подборе насосного оборудования. Разработаны математические модели, позволяющие сократить затраты времени и финансов на проектные и доводочные работы, за счет более широкого применения численных экспериментов при решении прямых и обратных гидродинамических задач.
Литература
1. Сазонов Ю.А., Сазонова Р.В. Расчеты струйных насосов. Учебное пособие. - М.: ГАНГ, 1997. - 52 с.
2. Елисеев В.Н., Сазонова Р.В. Расчет рабочих характеристик жидкоструйного компрессора с учетом параметров силового насоса // Строительство нефтяных и газовых скважин на суше и на море. – 1996. №12. С. 22-24.
3. Сазонов Ю.А. Варианты преобразований уравнения Эйлера и математическая модель первого уровня для центробежного насоса // Бурение и нефть. – 2008. №10. С. 33-35.
4. Сазонов Ю.А. Компьютерные технологии для разработки лопастных насосов // Нефть, газ и бизнес. - 2008. №11. С. 68-71.
5. Абрамович Г.Н. Прикладная газовая динамика. В 2 ч. Ч.1 // М.: Наука. 1991. 600 с.
6. Городивский А.В. Повышение эффективности насосно-эжекторных установок для утилизации нефтяных газов. Автореферат диссертации на соискание ученой степени кандидата технических наук. – М.: ВНИИГАЗ. 1986. 21 с.

